Java Prime Numbers examples
The following Java examples will print a list of all the prime numbers up to 1,000:
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71
73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173
179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281
283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409
419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541
547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659
661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809
811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941
947 953 967 971 977 983 991 997
Total: 168
3 Java examples:
- Java 8 Stream and BigInteger
- Plain old Java
- Sieve of Eratosthenes algorithm
1. Java 8 Stream and BigInteger
1.1 Using Stream.
PrintPrimeNumber.java
package com.mkyong.test;
import java.util.List;
import java.util.stream.Collectors;
import java.util.stream.IntStream;
import java.util.stream.Stream;
public class PrintPrimeNumber {
public static void main(String[] args) {
long count = Stream.iterate(0, n -> n + 1)
.limit(1000)
.filter(TestPrime::isPrime)
.peek(x -> System.out.format("%s\t", x))
.count();
System.out.println("\nTotal: " + count);
}
public static boolean isPrime(int number) {
if (number <= 1) return false; // 1 is not prime and also not composite
return !IntStream.rangeClosed(2, number / 2).anyMatch(i -> number % i == 0);
}
}
1.2 Using BigInteger::nextProbablePrime
Stream.iterate(BigInteger.valueOf(2), BigInteger::nextProbablePrime)
.limit(168)
.forEach(x -> System.out.format("%s\t", x));
Or BigInteger.TWO for Java 9
Stream.iterate(BigInteger.TWO, BigInteger::nextProbablePrime)
.limit(168)
.forEach(x -> System.out.format("%s\t", x));
2. Plain old Java
No more Java 8 Stream, back to basic.
PrintPrimeNumber2.java
package com.mkyong.test;
import java.util.ArrayList;
import java.util.List;
public class PrintPrimeNumber2 {
public static void main(String[] args) {
List<Integer> collect = new ArrayList<>();
for (int i = 0; i < 1000; i++) {
if (isPrime(i)) {
collect.add(i);
}
}
for (Integer prime : collect) {
System.out.format("%s\t", prime);
}
System.out.println("\nTotal: " + collect.size());
}
private static boolean isPrime(int number) {
if (number <= 1) return false; // 1 is not prime and also not composite
for (int i = 2; i * i <= number; i++) {
if (number % i == 0) {
return false;
}
}
return true;
}
}
3. Sieve of Eratosthenes
This Sieve of Eratosthenes algorithm is very fast to find all prime numbers.
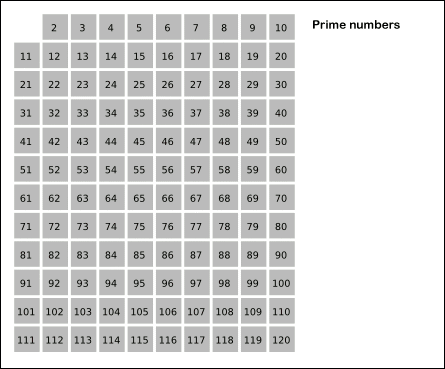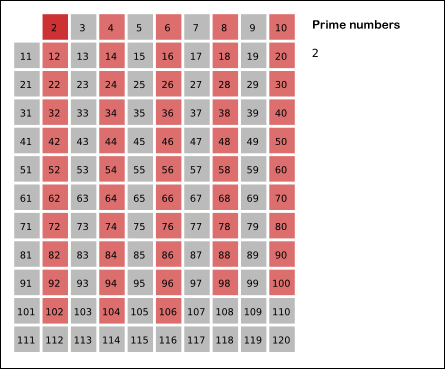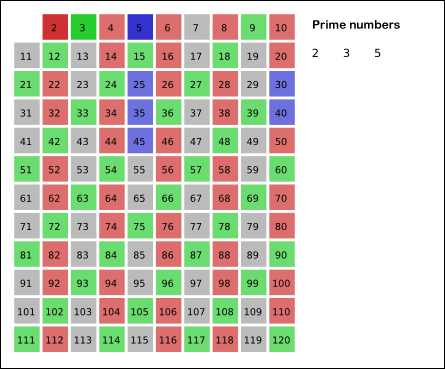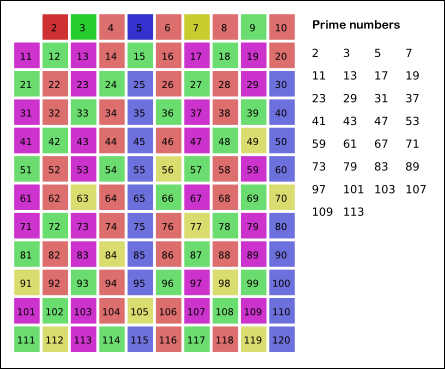
P.S Image is from Wikipedia
The concept is like this:
- Loop 1#
p=2= true, next 4,6,8,10,12,14…limit, all +2 set false - Loop 2#
p=3= true, next 6{false,1#,ignore},9,12{false,1#,ignore},15,18{false,1#,ignore},21…limit, all +3 set false - Loop 3#
p=4= {false,1#,ignore} - Loop 4#
p=5= true, next 10{false,1#,ignore},15{false,2#,ignore},20{false,1#,ignore}… all +5 set false - Loop 5#
p=6= {false,1#,ignore} - Loop… until limit, same idea.
- Collect all true = prime number.
PrintPrimeNumber3
package com.mkyong.test;
import java.util.Arrays;
import java.util.BitSet;
import java.util.LinkedList;
import java.util.List;
public class PrintPrimeNumber3 {
public static void main(String[] args) {
List<Integer> result = primes_soe_array(1000);
result.forEach(x -> System.out.format("%s\t", x));
System.out.println("\nTotal: " + result.size());
}
/**
* Sieve of Eratosthenes, true = prime number
*/
private static List<Integer> primes_soe(int limit) {
BitSet primes = new BitSet(limit);
primes.set(0, false);
primes.set(1, false);
primes.set(2, limit, true);
for (int p = 2; p * p <= limit; p++) {
if (primes.get(p)) {
for (int j = p * 2; j <= limit; j += p) {
primes.set(j, false);
}
}
}
List<Integer> result = new LinkedList<>();
for (int i = 0; i <= limit; i++) {
if (primes.get(i)) {
result.add(i);
}
}
return result;
}
// Some developers prefer array.
public static List<Integer> primes_soe_array(int limit) {
boolean primes[] = new boolean[limit + 1];
Arrays.fill(primes, true);
primes[0] = false;
primes[1] = false;
for (int p = 2; p * p <= limit; p++) {
if (primes[p]) {
for (int j = p * 2; j <= limit; j += p) {
primes[j] = false;
}
}
}
List<Integer> result = new LinkedList<>();
for (int i = 0; i <= limit; i++) {
if (primes[i]) {
result.add(i);
}
}
return result;
}
}
Can anyone help to convert above algorithm into a pure Java 8 Stream? 🙂
hey @mkyong!!
Thanks for the explanation and below is the way I used to print the prime series using java 8.